Assistant Professor
Universidad de Talca
A few things about me
I'm from Chile. I have a B.Sc. in Engineering Mathematics and a Mathematical Engineering professional degree (which is kind of equivalent to a Ms.Sc. in Mathematics) from the Departamento de Ingeniería Matemática at the Universidad de Chile, where I worked under the supervision of Juan Dávila on a singular perturbation problem. The thesis (in spanish) and the article that I wrote about the subject can be found in my publication list. I completed my Ph.D. in Mathematics studies at the Mathematics Department from Rutgers University with Haim Brezis as my advisor. My thesis is the compilation of the research I did while at Rutgers about singular Sturm-Liouville equations. You can find the thesis and the respective papers in my publication list.
Currently I am an Assistant Professor at the Instituto de Matemáticas from the Universidad de Talca where I teach both undergraduate and graduate courses. My current research interests are degenerate/singular elliptic equations together with some aspects related to weighted Sobolev spaces, you can see more details by clicking the Research and Publications links from the side panel.
Academic Positions
-
Present 2014
-
2014 2013
Instructor
Universidad de Talca
-
2013 2012
Postdoc
Universidad de Talca
Education & Training
-
Ph.D. 2012
Ph.D. in Mathematics
Rutgers University
-
M.E.2006
Mathematical Engineering
Universidad de Chile
-
B.Sc.2006
Bachelor of Sciences in Engineering Mathematics
Universidad de Chile
Honors, Scholarships and Grants
-
2018-2022FONDECYT Regular Grant
Grant awarded by the Chilean government. -
2014-2017FONDECYT Iniciación Grant
Grant awarded by the Chilean government.
-
2007-2012Beca Gestión Propia
Scholarship awarded by the Chilean government. -
2000-2006Beca Universidad de Chile
Scholarship awarded by the University of Chile.
-
2000-2005Dean's List
Recognition awarded by the Engineering School to the best students of the year.
Research Summary
Interests
- Elliptic partial differential equations
- Sobolev spaces
- Hardy-type inequalities
- Singular Sturm-Liouville equations
Research Projects
-
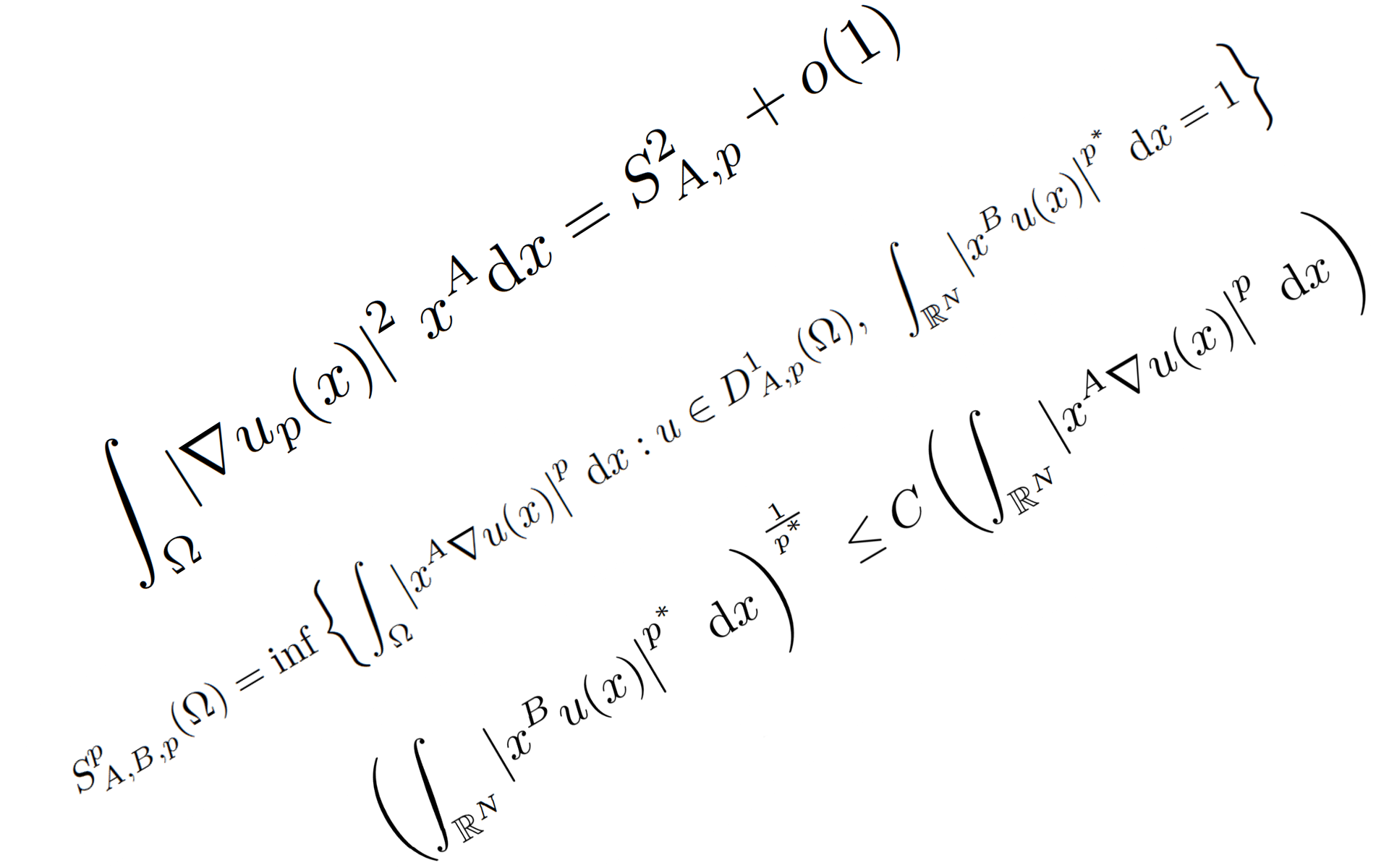
In the past years I have been studying singular (degenerate) second order elliptic operators such as the singular Sturm-Liouville operator \(L_\alpha u(t):=-(t^{2\alpha}u'(t))'\) where \(\alpha>0\), or the degenerate elliptic operator \(\mathcal L_\alpha u(x):=-\mathrm{div}(x^A\nabla u(x))\) where \(A\in\mathbb R^N\) is a given vector and \(x^A=|x_1|^{a_1}\cdot\ldots |x_N|^{a_N}\). In such studies the construction of suitable weighted Sobolev spaces and the study of their properties were quite significant and opened a very interesting line of research. In particular, it was established the validity of the following Hardy-Sobolev inequalities \begin{equation}\label{hs-ineq} \left(\int_{\mathbb R^N} \left|x^B u(x)\right|^{p^*} dx\right)^{\frac 1{p^*}}\leq C\left(\int_{\mathbb R^N}\left|x^A\nabla u(x)\right|^p dx\right)^{\frac1p} \end{equation} for suitable \(p\geq 1\), \(A,B\in\mathbb R^N\) and \[ p^*=\frac{Np}{N-p(1+b-a)}, \] where \(a=a_1+\ldots+a_N\) and \(b=b_1+\ldots+b_N\). This work leads to several interesting open problems, some of which are the purpose of this research project.
One of the natural topics of interest that arise when one has proved such an inequality is the existence of extremals and the value of the best possible constant \(C>0\). Namely, for a given open set \(\Omega\subseteq\mathbb R^N\), we would like to investigate the existence of a function \(u_{A,B,p}=u_p\) and the value of the constant \(S_{A,B,p}>0\) such that \[ S_{A,B,p}^p(\Omega)=\inf\left\{\int_{\Omega}\left|x^A\nabla u(x)\right|^p dx:~u\in D^1_{A,p}(\Omega),~\int_{\mathbb R^N} \left|x^B u(x)\right|^{p^*} dx=1\right\}=\int_{\Omega}\left|x^A\nabla u_p(x)\right|^p dx, \] here \(D^1_{A,p}(\Omega)\) denotes the completion of \(C^\infty_0(\Omega)\) under the norm \(\Vert u\Vert^p=\int_{\Omega}\left|x^A\nabla u(x)\right|^p dx\). The main difficulty in this problem arises when one notices that \(p^*\) is critical from the viewpoint of the embedding of the weighted Sobolev space into the weighted \(L^q\) space. More precisely, if \(\Omega\) is bounded and contains the origin then the space \(D^1_{A,p}(\Omega)\) is embedded into the respective weighted space \(L^q(\Omega, x^{Bp^*})\) for \(1\leq q\leq p^*\), but the embedding is compact if and only if \(q<{p^*}\). This lack of compactness prevents us from using the classical minimization strategy to obtain extremals for \(S_{A,B,p}(\Omega)\), thus making this a problem worth addressing.
The other problem we plan to attack in this research project concerns the the asymptotic behavior of minimizer sequences for the problem \[ S^p_{A,p}=\inf\left\{\int_{\Omega}\left|\nabla u(x)\right|^2x^A dx:u\in D^1_{A,2}(\Omega),~\int_{\Omega} \left|u(x)\right|^{p}x^A dx=1\right\} \] where \(p\nearrow 2^*\). More precisely, since the embedding from \(D^1_{A,2}(\Omega)\) to \(L^p(\Omega,x^Adx)\) is compact for \(q<{2^*}\) we can assert the existence of a function \(u_{A,p}=u_p\in D^1_{A,2}(\Omega)\) such that \(\int_{\Omega} \left|u(x)\right|^{p}x^A dx=1\) and \[ \int_{\Omega}\left|\nabla u_p(x)\right|^2x^A dx=S^2_{A,p}+o(1) \] as \(p\nearrow 2^*\). The idea is to obtain a generalization of the known results about the classical Sobolev inequality (\(A=0\)). For example, we would like to know if \(u_p\) develops blow up points as \(p\nearrow 2^*\), and if this is the case, we would also like to discover the location of such blow up points and the respective limiting profile of suitable normalized minimizers.
-
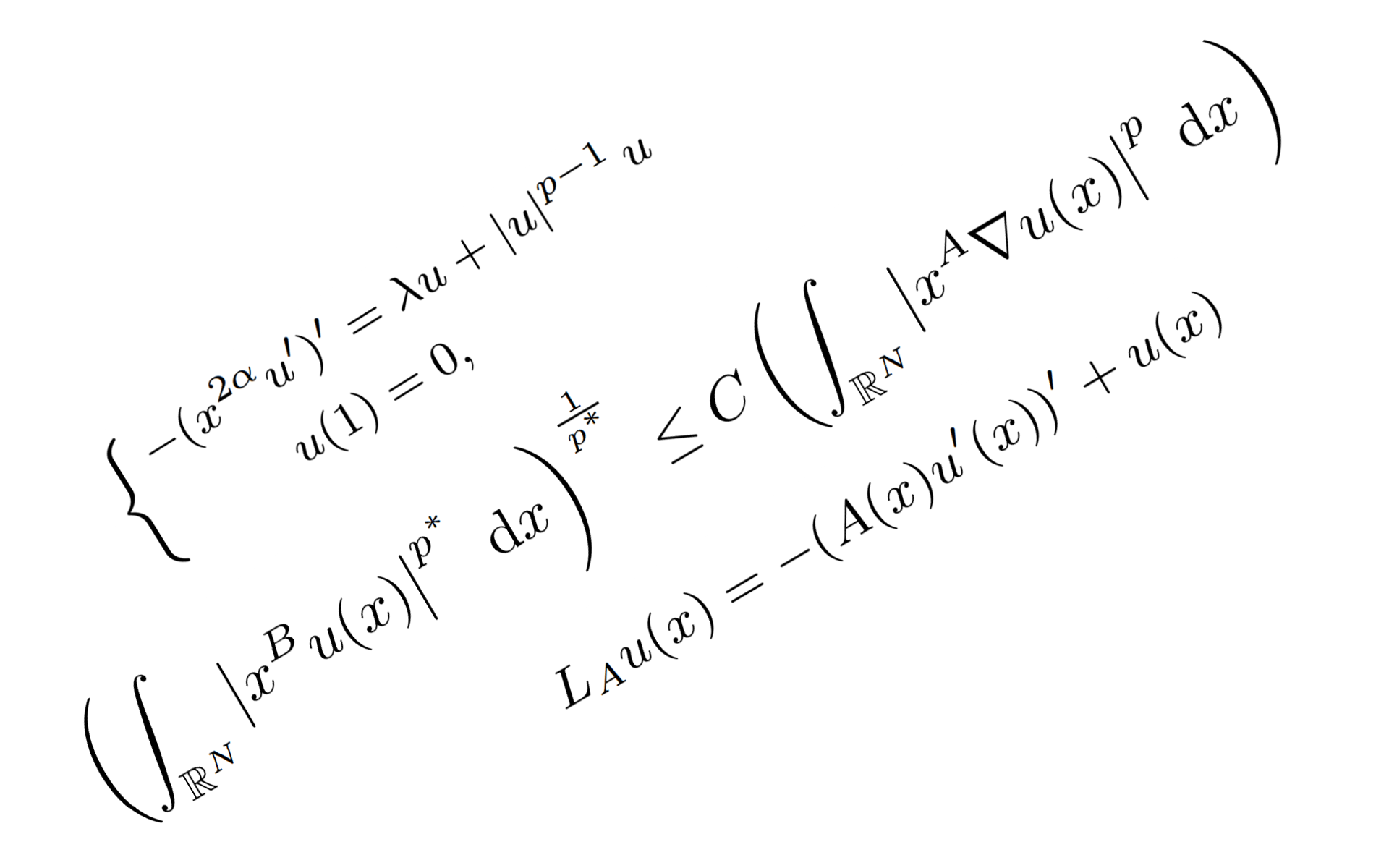
During the course of my Ph.D. studies, I developed a theory about the singular second order Sturm-Liouville operator \(L_\alpha u(x)=-(x^{2\alpha}u'(t))'\) on the interval \((0,1)\), where \(\alpha>0\) is a real parameter. One of the main reasons I studied this operator is that it serves as a toy model to more general degenerate elliptic operators, and results obtained in this simpler setup might shed some light into the study of more general cases.
In joints works with H. Wang we used tools from functional analysis to prove existence and regularity, uniqueness of solutions, as-well as spectral properties of the equation \(L_\alpha u+u=f\). The core idea behind this study was to look for solutions in appropriate weighted Sobolev spaces (which had to be constructed for the occasion). Later, I studied the semi-linear eigenvalue problem \(L_\alpha u=\lambda u+|u|^{p-1}u\), where \(\lambda\) and \(p>1\) are real parameters. In those works, I performed a bifurcation analysis for \(L_\alpha\), determining the relationship between the parameters \(\alpha,~\lambda\) and \(p\) and the existence/non-existence of a branch of positive solutions emanating form the first eigenvalue \(\lambda_1\) of \(L_\alpha\).
The main goal of this work will be to continue the research about the operator \(L_\alpha\) by answering some of the open problems that arose in the works cited before.
In terms of the semi-linear eigenvalue problem \(L_\alpha u=\lambda u+|u|^{p-1}u\) the open problems I plan to attack can be divided into two cases with respect to the parameter \(\alpha\): \(0 < \alpha<1\) and \(\alpha\geq 1\). In the case where \(0<\alpha<1\) there are a few open questions, specially when the parameter \(p\) is large: in a previous article we showed that positive solutions only exist in a range \(\hat\lambda<\lambda<\lambda_1\) for some \(\hat\lambda>0\), however we still do not have a precise description of the optimal \(\hat\lambda\), and how the branch of positive solutions behave near that \(\hat\lambda\). When \(\alpha\geq 1\), we know that all solutions satisfying \(u(1)=0\) must have infinite sing changes in the interval \((0,1)\), however, we would like to know how fast the sing changes occur as we approach \(x=0\); also, the existence of bounded solutions in this case remain an open question.
On the other hand, the operator \(L_\alpha u(x)=-(x^{2\alpha}u'(x))'\) can be generalized into two different directions:
- We can consider the operator \(L_A u(x):=-(A(x)u'(x))'\), where \(A(x)\) is a non-negative function that looks like \(x^{2\alpha}\) near \(x=0\), and try to study the spectral properties of such operator. The main problem I plan to address occurs when \(\alpha=1\): we would like to describe the spectrum of the operator \(\mathcal L_A\), in particular, finding conditions on \(A(x)\) for the existence/non-existence of eigenvalues has proven to be quite challenging (see the works of Stuart and Villaume for the case \(\alpha=1\)).
- We can consider an elliptic operator in \(N+1\) dimensions of the form \(L_A u(x,y):=-\mathrm{div}(A(y)\nabla u(x,y))\), where \((x,y)\in \Omega\times(0,M)\), \(\Omega\subset \mathbb{R}^N\), \(0
Publications and preprints
Filter by type:
Sort by year:
Abstract
In this article we study the quasi-linear equation \[ \left\lbrace \begin{aligned} \mathrm{div} \mathcal A(x,u,\nabla u)&=\mathcal B(x,u,\nabla u)&&\text{in }\Omega,\\ u\in H^{1,p}_{loc}&(\Omega;wdx), \end{aligned} \right. \] where \(\mathcal A\) and \(\mathcal B\) are functions satisfying \(\mathcal A(x,u,\nabla u)\sim \mathcal B(x,u,\nabla u)\sim w(|\nabla u|^{p-2}\nabla u+|u|^{p-2}u)\) for \(p>1\) and a \(p\)-admissible weight function \(w\). We establish interior regularity results of weak solutions and use those results to obtain point-wise asymptotic estimates for solutions to \[ \left\lbrace \begin{aligned} -\mathrm{div}(w|\nabla u|^{p-2}\nabla u)&=w|u|^{q-2}u&&\text{in }\Omega,\\ u\in D^{1,p,w}&(\Omega) \end{aligned} \right. \] for a critical exponent \(q>p\) in the sense of Sobolev.
Poincaré's inequality and Sobolev spaces with monomial weights
Article
Mathematische Nachrichten 296 (2023), 4500--4522. Partially funded by FONDECYT Regular 1180516.
Abstract
In this article we use a weighted version of Poincaré's inequality to study density and extension properties of weighted Sobolev spaces over some open set \(\Omega\subseteq\mathbb{R}^N\). Additionally, we study the specific case of monomial weights \[ w(x_1,\ldots,x_N)=\prod_{i=1}^N|x_i|^{a_i},\ a_i\geq 0, \] showing the validity of a weighted Poincaré inequality together with some embedding properties of the associated weighed Sobolev spaces.
Extremals for Hardy-Sobolev type inequalities with monomial weights
Article
Journal of Mathematical Analysis and Applications 494 (2021), 124645. Partially funded by FONDECYT Regular 1180516.
Abstract
In this article we study the existence and non-existence of extremals for the following family of Hardy-Sobolev inequalities \[ \left({\int_{(\mathbb R_+)^k\times{\mathbb R}^{N-k}}|x^B u|^{q}}\right)^{\frac{1}{q}}\leq C\left({\int_{(\mathbb R_+)^k\times\mathbb R^{N-k}}|x^A \nabla u|^{p}}\right)^{\frac{1}{p}}, \] which holds for suitable values of \(A,~B\in\mathbb R^N\), \(q>p>1\). Here the quantity \(x^A\) (respectively \(x^B\)) denotes the monomial weight defined as \[ x^A=|x_1|^{a_1}\cdot\ldots\cdot |x_k|^{a_k}\quad \text{(respectively } x^B=|x_1|^{b_1}\cdot\ldots\cdot |x_k|^{b_k}\text{)}. \]
The essential spectrum of a singular Sturm-Liouville operator
Article
Mathematische Nachrichten 291 (2018), 593-609. Partially funded by FONDECYT Iniciación 11140002.
Abstract
In this paper we study the essential spectrum of the operator \[ L_Au(x)=-(A(x)u'(x))'+u(x) \] where \(A(x)\) is a positive absolutely continuous function on \((0,1)\) that resembles \(x^{2\alpha}\) for some \(\alpha\geq 1\). We prove that the essential spectrum of \(L_A\) coincides with the essential spectrum of the operator \(L_\alpha u(x):=-(x^{2\alpha}u'(x))'+u(x)\).
Uniqueness results for a singular non-linear Sturm-Liouville equation
Article
Houston Journal of Mathematics 42 (2016), 285--306. Partially funded by NSF Grant DMS 1207793.
Abstract
In this work we study the uniqueness of solutions to the following singular non-linear Sturm-Liouville equation \[ \left\lbrace\begin{aligned} -(x^{2\alpha}u')'&=\lambda u + u^p &\hbox{in } (0,1),\\ u&>0 &\hbox{in } (0,1),\\ u(1)&=0, \end{aligned}\right. \] where \(0<\alpha<1\), \(p>1\) and \(\lambda\in\mathbb R\) are parameters.
We show that when \(0<\alpha\leq \frac12\) and \(p>1\), and when \(\frac12<\alpha<1\) and \(1 < p \leq\frac{3-2\alpha}{2\alpha-1}\) uniqueness of solutions is guaranteed to hold when one imposes some appropriate behavior at the origin.
Hardy-Sobolev-type inequalities with monomial weights
Article
Annali di Matematica Pura ed Applicata (1923 -) 196 (2017), 579--598. Partially funded by FONDECYT Iniciación 11140002.
Abstract
We give an elementary proof of a family of Hardy-Sobolev-type inequalities with monomial weights. As a corollary, we obtain a weighted trace inequality related to the fractional Laplacian.
Asymptotic estimates for the least energy solution of a planar semi-linear Neumann problem
Article
Journal of Mathematical Analysis and Applications 428 (2015), 258--281. Partially funded by PIA ACT 56.
Abstract
In this work we study the asymptotic behavior of the \(L^\infty\) norm of the least energy solution \(u_p\) of the following semi-linear Neumman problem \[ \left\lbrace\begin{aligned} \Delta u = u&,\; u>0 &&\text{in }\Omega,\\ \frac{\partial u}{\partial \nu} &=u^p &&\text{on }\partial\Omega,\\ \end{aligned}\right. \] where \(\Omega\) is a smooth bounded domain in \(\mathbb R^2\). Our main result shows that the \(L^\infty\) norm of \(u_p\) remains bounded, and bounded away from zero as \(p\) goes to infinity, more precisely, we prove that \[ \lim\limits_{p\to\infty}\Vert u\Vert_{L^\infty(\partial\Omega)}=\sqrt e. \]
Please check the addendum where an additional remark has been included in page 8.
Oscillations in a semi-linear singular Sturm-Liouville equation
Article
Asymptotic Analysis 94 (2015), 363--373. Partially funded by FONDECYT Iniciación 11140002.
Abstract
We study the semi-linear Sturm-Liouville equation \[ \left\lbrace\begin{aligned} -(x^{2\alpha}u')'&=\lambda u + |u|^{p-1}u &\hbox{in } (0,1),\\ u(1)&=0, \end{aligned}\right. \] where \(\alpha\geq 1\), \(p>1\), and \(\lambda\) are real parameters. We prove that all non-trivial solutions are oscillatory and unbounded as \(x\) approaches \(0\). Moreover, there exist \(\gamma>0\) and \(\delta>0\) such that any solution \(u(x)\) resembles \(x^{-\gamma}\eta(x^{-\delta})\) near the origin, where \(\eta\) is a non-trivial periodic solution to the Emden-Fowler equation \(\delta^2\eta''+|\eta|^{p-1}\eta=0\) in \([0,\infty)\).
Bifurcation analysis of a singular nonlinear Sturm-Liouville equation
Article
Communications in Contemporary Mathematics 16 (2014), 1450012 (54 pages). Partially funded by NSF Grant DMS 1207793.
Abstract
In this paper we study existence of positive solutions to the following singular non-linear Sturm-Liouville equation \[ \left\lbrace\begin{aligned} -(x^{2\alpha}u')'&=\lambda u + u^p \hbox{ in } (0,1),\\ u(1)&=0,\\ \end{aligned}\right. \] where \(\alpha>0\), \(p>1\) and \(\lambda\) are real constants.
We prove that when \(0<\alpha\leq\frac12\) and \(p>1\) or when \(\frac12<\alpha<1\) and \(1 < p\leq \frac{3-2\alpha}{2\alpha-1}\), there exists a branch of continuous positive solutions bifurcating to the left of the first eigenvalue of the operator \(\mathcal L_\alpha u=-(x^{2\alpha}u')'\) under the boundary condition \(\lim\limits_{x\to0}x^{2\alpha}u'(x)=0\). The projection of this branch onto its \(\lambda\) component is unbounded in two cases: when \(0<\alpha\leq\frac12\) and \(p>1\), and when \(\frac12<\alpha<1\) and \(p<\frac{3-2\alpha}{2\alpha-1}\). On the other hand, when \(\frac12<\alpha<1\) and \(p\geq\frac{3-2\alpha}{2\alpha-1}\), the projection of the branch has a positive lower bound below which no positive solution exists.
When \(0<\alpha<\frac12\) and \(p>1\), we show that a second branch of continuous positive solution can be found to the left of the first eigenvalue of the operator \(\mathcal L_\alpha\) under the boundary condition \(\lim\limits_{x\to 0}u(x)=0\).
Finally, when \(\alpha\geq1\), the operator \(\mathcal L_\alpha\) has no eigenvalues under its canonical boundary condition at the origin, and we prove that in fact there are no positive solutions to the equation, regardless of \(\lambda\in \mathbb R\) and \(p>1\).
A Hardy type inequality for \(W^{m,1}_0(\Omega)\) functions
Article
Journal of the European Mathematical Society (JEMS) 15 (2013), 145--155. Partially funded by NSF Grant DMS 0802958.
Abstract
We consider functions \(u\in W^{m,1}_0(\Omega)\), where \(\Omega\subset \mathbb R^N\) is a smooth bounded domain, and \(m\geq 2\) is an integer. For all \(j\geq 0\), \(1\leq k\leq m-1\), such that \(1\leq j+k\leq m\), we prove that \(\frac{\partial^ju(x)}{d(x)^{m-j-k}}\in W^{k,1}_0(\Omega)\) with \[ \left\Vert\partial^k\left(\frac{\partial^ju(x)}{d(x)^{m-j-k}}\right)\right\Vert_{L^1(\Omega)}\leq C\left\Vert u\right\Vert_{W^{m,1}(\Omega)}, \] where \(d\) is a smooth positive function which coincides with \(\mathrm{dist}(x,\partial\Omega)\) near \(\partial\Omega\), and \(\partial^l\) denotes any partial differential operator of order \(l\).
A singular Sturm-Liouville equation under non-homogeneous boundary conditions
Article
Differential Integral Equations 25 (2012), 85--92. Partially funded by NSF Grant DMS 0802958.
Abstract
Given \(\alpha>0\) and \(f\in L^2(0,1)\), consider the following singular Sturm-Liouville equation, \[ \left\lbrace\begin{aligned} -(x^{2\alpha}u'(x))'+u(x)&=f(x) \hbox{ a.e. on } (0,1),\\ u(1)&=0. \end{aligned}\right. \] We prove existence of solutions under (weighted) non-homogeneous boundary conditions at the origin.
A Hardy type inequality for \(W^{2,1}_0(\Omega)\) functions
Article
Comptes Rendus Mathématique. Académie des Sciences. Paris 349 (2011), 765--767. Partially funded by NSF Grant DMS 0802958.
Abstract
We consider functions \(u\in W^{2,1}_0(\Omega)\), where \(\Omega\subset \mathbb R^N\) is a smooth bounded domain. We prove that \(\frac{u(x)}{d(x)}\in W^{1,1}_0(\Omega)\) with \[ \left\Vert \nabla\left(\frac{u(x)}{d(x)}\right)\right\Vert_{L^1(\Omega)}\leq C\left\Vert u\right\Vert_{W^{2,1}(\Omega)}, \] where \(d\) is a smooth positive function which coincides with \(\mathrm{dist}(x,\partial\Omega)\) near \(\partial\Omega\) and \(C\) is a constant depending only on \(\Omega\).
A singular Sturm-Liouville equation under homogeneous boundary conditions
Article
Journal of Functional Analysis 261 (2011), 1542--1590. Partially funded by NSF Grant DMS 0802958.
Abstract
Given \(\alpha>0\) and \(f\in L^2(0,1)\), we are interested in the equation \begin{equation*} \left\lbrace\begin{aligned} -(x^{2\alpha}u'(x))'+u(x)&=f(x) \hbox{ on } (0,1],\\ u(1)&=0. \end{aligned}\right. \end{equation*} We prescribe appropriate (weighted) homogeneous boundary conditions at the origin and prove the existence and uniqueness of \(H^2_{loc}(0,1]\) solutions. We study the regularity at the origin of such solutions. We perform a spectral analysis of the differential operator \(\mathcal{L}u:=-(x^{2\alpha}u')'+u\) under those appropriate homogenous boundary conditions.
A Hardy type inequality for \(W^{m,1}(0,1)\) functions
Article
Calculus of Variations and Partial Differential Equations 39 (2010), 525--531. Partially funded by NSF Grant DMS 0802958.
Abstract
In this paper, we consider functions \(u\in W^{m,1}(0,1)\) where \(m\geq 2\) and \(u(0)=Du(0)=\ldots=D^{m-1}u(0)=0\). Although it is not true in general that \(\frac{D^ju(x)}{x^{m-j}}\in L^1(0,1)\) for \(j\in\{0,1,\ldots,m-1\}\), we prove that \(\frac{D^ju(x)}{x^{m-j-k}}\in W^{k,1}(0,1)\) if \(k\geq 1\) and \(1\leq j+k\leq m\), with \(j,k\) integers. Furthermore, we have the following Hardy type inequality, \[ \left\Vert D^k\left(\frac{D^ju(x)}{x^{m-j-k}}\right)\right\Vert_{L^1(0,1)}\leq \frac {(k-1)!}{(m-j-1)!}\left\Vert D^mu\right\Vert_{L^1(0,1)}, \] where the constant is optimal.
Solutions with spikes at the boundary for a 2D nonlinear Neumann problem with large exponent
Article
Journal of Differential Equations 246 (2009), 2991--3037.
Abstract
We consider the elliptic equation \(-\Delta u+u=0\) in a bounded, smooth domain \(\Omega\) in \(\mathbb R^2\), subject to the nonlinear Neumann boundary condition \(\frac{\partial u}{\partial \nu}=u^p\). Here \(p>1\) is a large parameter. We prove that given any integer \(m\ge 1\) there exist at least two families of solutions \(u_p\) developing exactly \(m\) peaks \(\xi_i \in \partial\Omega\), in the sense that \[pu^p\rightharpoonup 2e\pi\sum\limits_{i=1}^{m}\delta_{\xi_i},\] as \(p\rightarrow\infty\).
On some singular Sturm-Liouville equations and a Hardy type inequality
Thesis
Rutgers University, 185+viii pages. Ph. D. Thesis. Partially funded by NSF Grants DMS 0802958 and DMS 1207793.
Abstract
The main body of this dissertation can be divided into two separate topics. The first topic deals with a Hardy type inequality for functions belonging to the Sobolev space \(W^{m,1}_0(\Omega)\), where \(m\geq 2\) and \(\Omega\) is a smooth bounded domain in \(\mathbb R^N\), \(N\geq 1\). We show that for such functions \(u\in W^{m,1}_0(\Omega)\), one has \[ \left\Vert\partial^k\left(\frac{\partial^ju(x)}{d(x)^{m-j-k}}\right)\right\Vert_{L^1(\Omega)}\leq C\Vert u\Vert_{W^{m,1}(\Omega)}, \] where \(j,k\) are non-negative integers such that \(1 \leq k \leq m-1\) and \(1\leq j+k\leq m\), and \(d(x)\) is a smooth positive function which coincides with \(\mathrm{dist}(x,\partial\Omega)\) near \(\partial\Omega\).
The second topic deals with the study of the singular Sturm-Liouville operator \(\mathcal L_\alpha u:=-(x^{2\alpha}u')'\), where \(\alpha>0\). We develop a linear theory for such operator by introducing suitable weighted Sobolev spaces and prove existence and uniqueness for equations of the form \(\mathcal L_\alpha u+u=f\in L^2\) under both homogeneous and non-homogeneous boundary data at the origin. In addition, the spectrum of the operator \(\mathcal L_\alpha\) is fully described.
Finally, we prove existence, non-existence and uniqueness results for positive solutions of the non-linear singular Sturm-Liouville equation \(\mathcal L_\alpha u=\lambda u+u^p,\ u(1)=0\), where \(\alpha>0\), \(p>1\) and \(\lambda\in\mathbb R\) are parameters.
Concentración en un problema elíptico 2-dimensional con condiciones Neumann de exponente grande
Thesis
Universidad de Chile, 76+vii pages. Mathematical engineering thesis.
Abstract
En este trabajo de título se presenta un estudio de la ecuación \[ \begin{aligned} -\Delta u + u &= 0 &\text{en }\Omega\\ \frac{\partial u}{\partial \nu} &= u^p &\text{en }\partial\Omega, \end{aligned} \] donde \(\Omega\) es un dominio en el plano de frontera suave y \(p\) es un parámetro que tiende a infinito. Tal estudio tiene como objetivo final probar la existencia de una familia de soluciones que presenten concentración en puntos de la frontera de \(\Omega\).
Para obtener tal resultado, se ha procedido siguiendo un esquema de reducción finito-dimensional, lo que consiste, en términos generales, en buscar una solución de la forma \(U+\phi\), donde \(U\) es una función escogida adecuadamente y \(\phi\) es un término de ajuste, cuya existencia está ligada a un problema en dimensión finita. El marco analítico funcional planteado, presenta grandes similitudes con trabajos anteriores, en particular, con el utilizado por Esposito, Musso y Pistoia en un problema interior análogo al que aquí se estudia.
La primera parte de esta memoria trata con la elección de una buena aproximación inicial, la función \(U\), de modo que se tenga el comportamiento asintótico esperado, y que el error obtenido sea lo suficientemente pequeño. El trabajo continúa al reescribir la ecuación original, para obtener una ecuación no-lineal en términos de \(\phi\). Para estudiar dicha ecuación, primero se realiza un completo análisis de la invertibilidad de un problema lineal asociado. En segundo lugar, se analiza la existencia en una ecuación no-lineal auxiliar vía un esquema de punto fijo, entregando, además, las condiciones necesarias de regularidad sobre la solución para reducir el problema de existencia de soluciones del problema original, al de encontrar puntos críticos de una función finito-dimensional. Finalmente, demostramos que dicha función finito-dimensional admite al menos dos puntos críticos y que tales puntos críticos resultan ser los puntos en donde se produce concentración.
Finalmente, se formulan algunas interrogantes respecto a posibles mejoras en el resultado obtenido. Así también, siguiendo lo realizado por Adimurthi y Grossi, como lo desarrollado en trabajos de Ren y Wei respecto al problema interior asociado, se conjeturan ciertos resultados que se podrían obtener respecto al comportamiento asintótico de la solución de mínima energía de este problema.
Teaching
Here you can find some teaching material (lecture notes, exercises, past exams) from the courses I have taught. Most of the material is in spanish.
Course List
-
3/2024Matemática (C.P.A.)
Curso anual en donde se entrega una formación básica en álgebra y cálculo diferencial . -
3/2024Matemática (Auditoría)
Curso anual en donde se entrega una formación básica en álgebra y cálculo diferencial . -
3/2024Análisis Funcional
Curso trimestral, para el magíster y doctorado, en donde se introducen las herramientas fundamentales del análisis funcional. -
8/2023Matemáticas II (Tec. Médica)
Curso semestral en donde se estudian límites, derivadas e integrales.- Apunte
-
8/2023Cálculo I (Ing. Civil)
Curso semestral en donde se estudian funciones, límites y derivadas.- Apunte
-
6/2023Espacios de Sobolev y EDP
Curso trimestral, para el magíster y doctorado, en donde se introducen los espacios de Sobolev y el uso de estos para el estudio de ecuaciones diferenciales parciales. -
3/2023Cálculo II (Agronomía)
Curso semestral en donde se estudian integrales definidas, ecuaciones diferenciales y cálculo en varias variables.- Apunte
-
3/2023Matemáticas I (Ing. Inf. Empresarial)
Curso semestral en donde se introducen conceptos de lógica, conjuntos, principios de conteo y matrices. -
1/2023Teoremas de punto fijo y ecuaciones diferenciales
Cursillo para la escuela de verano del Instituto de Matemáticas de la Universidad de Talca.- Apunte
-
8/2022Cálculo I (Ing. Civil) Curso semestral en donde se estudian funciones, límites y derivadas.
- Apunte
-
8/2022Matemáticas II (Adm. Pública)
Curso semestral en donde se estudian límites, derivadas e integrales.- Apunte
-
3/2022Cálculo II (Ing. Civil)
Curso semestral en donde se estudia integración en una variable y series.- Apunte
-
3/2022Cálculo (Ing. Comercial)
Curso semestral en donde se introducen los conceptos de integración, series, cálculo en varias variables y ecuaciones diferenciales.- Apunte
-
9/2021
-
6/2021
-
3/2021Análisis Funcional Curso trimestral, para el magíster y doctorado, en donde se introducen las herramientas fundamentales del análisis funcional.
-
9/2020
-
6/2020
-
3/2020Análisis Funcional Curso trimestral, para el magíster y doctorado, en donde se introducen las herramientas fundamentales del análisis funcional.
-
9/2019Métodos Variacionales
Curso trimestral, para el magíster y doctorado, en donde se revisan algunos resultados relativos a métodos variacionales y algunas aplicaciones al estudio de ecuaciones diferenciales parciales. -
8/2019
-
8/2019Ecuaciones Diferenciales Ordinarias (Ing. Civil)
Curso semestral en donde se estudian ecuaciones diferenciales ordinarias de primer orden, de orden superior, sistemas de EDOs lineales y la transformada de Laplace. -
3/2019
-
3/2019
-
9/2018Espacios de Sobolev y EDP Curso trimestral, para el magíster y doctorado, en donde se introducen los espacios de Sobolev y el uso de estos para el estudio de ecuaciones diferenciales parciales.
-
8/2018
-
8/2018
-
3/2018
-
3/2018
-
9/2017
-
6/2017
-
3/2017Análisis Funcional Curso trimestral, para el magíster y doctorado, en donde se introducen las herramientas fundamentales del análisis funcional.
-
1/2017El Teorema del punto fijo de Banach y aplicaciones
Mini curso para la escuela de verano del Instituto de Matemáticas de la Universidad de Talca. -
9/2016
-
6/2016
-
3/2016
-
8/2015Álgebra (Agronomía) Curso semestral donde se introducen conceptos de funciones en una variable real, límites, derivadas y algunas aplicaciones.
-
3/2015
-
3/2015
-
8/2014Álgebra (Agronomía)
Curso semestral donde se introducen conceptos de funciones en una variable real, límites, derivadas y algunas aplicaciones. -
3/2014
-
3/2014
-
1/2014Espacios de Sobolev con peso y EDOs singulares Mini curso para la escuela de verano del Instituto de Matemáticas de la Universidad de Talca.
- Apunte
-
8/2013Matemática Aplicada (Agronomía)
Curso semestral donde se incluyes modelos matemáticos aplicados a la agronomía, utilizando herramientas de cálculo, programación lineal y ecuaciones diferenciales.- Apunte
-
3/2013Matemática Aplicada (Agronomía) Curso semestral donde se incluyes modelos matemáticos aplicados a la agronomía, utilizando herramientas de cálculo, programación lineal y ecuaciones diferenciales.
- Apunte
